© 2023 Steven Obua

A First Look At Practal

by Steven Obua

Cite as https://practal.com/press/aflap/1 February 4, 2023

The first release of Practal as a Visual Studio Code Extension is out! It is an early and experimental release without its most crucial functionality of proving and computing, but it has syntax highlighting and the ability to define your own syntax. It is already possible to state declarations, definitions and axioms, and definitions are properly checked. So if you can write a theory without Practal flagging any problems, then you have authored a theory in Abstraction Logic! Of course, whether this theory makes any sense or not, depends on your axioms.

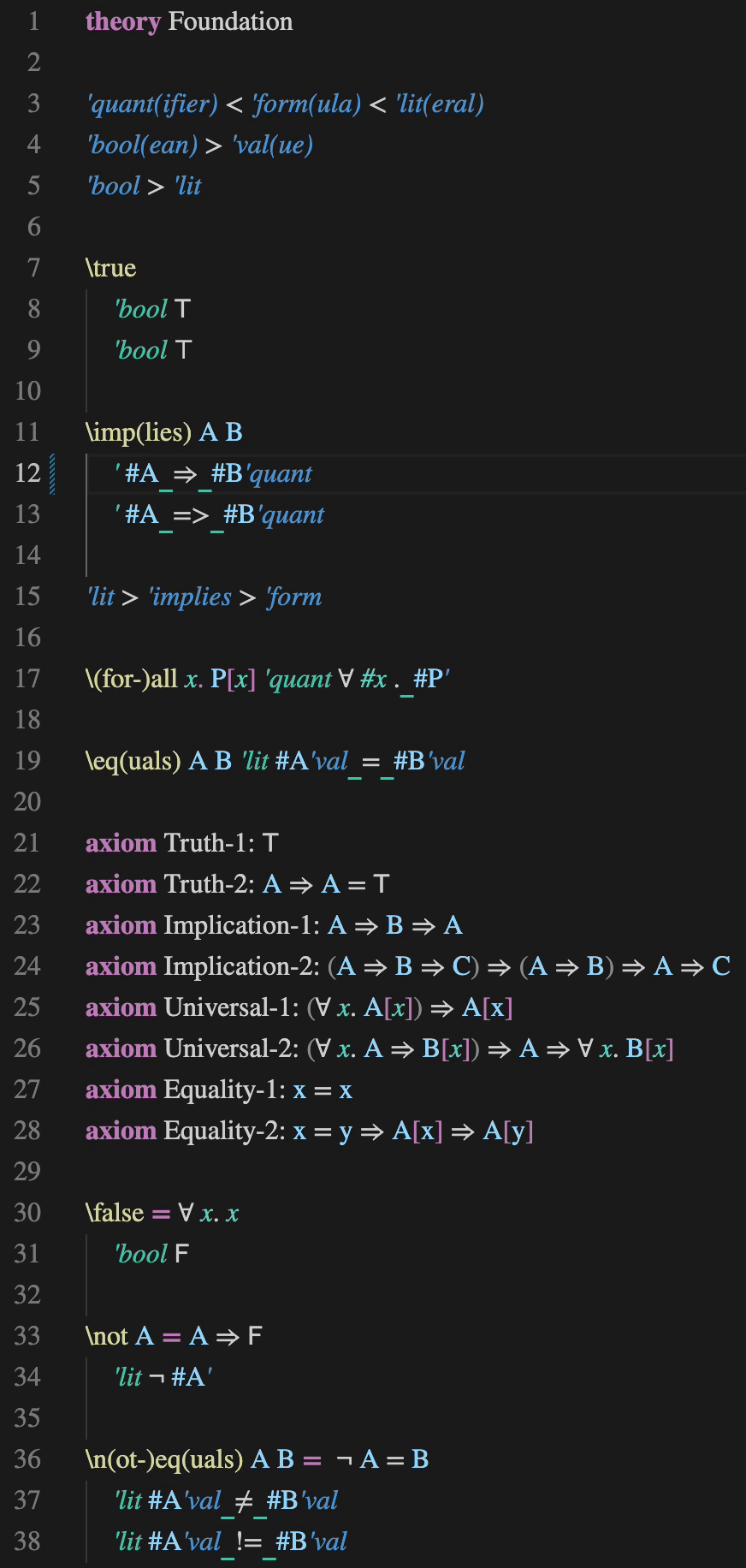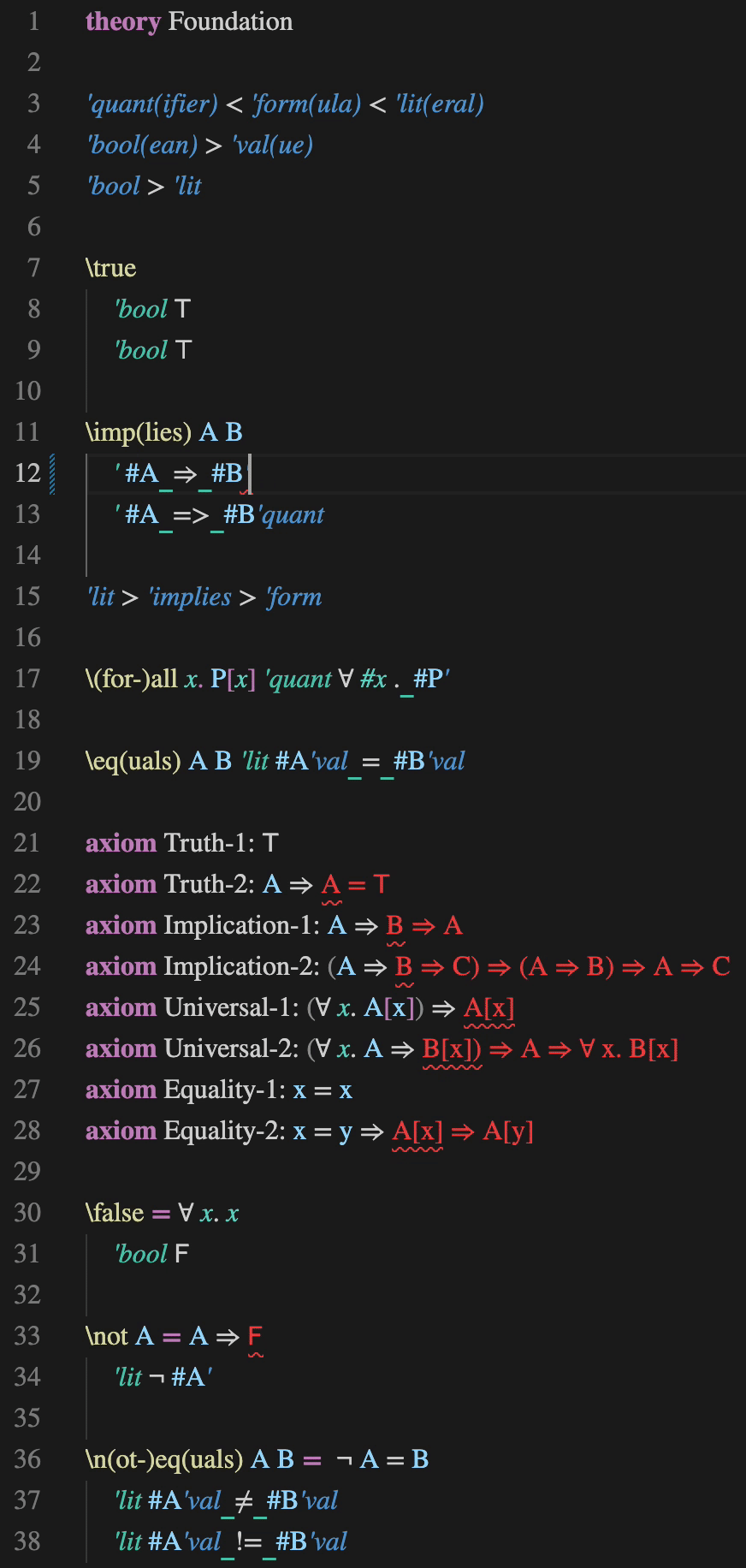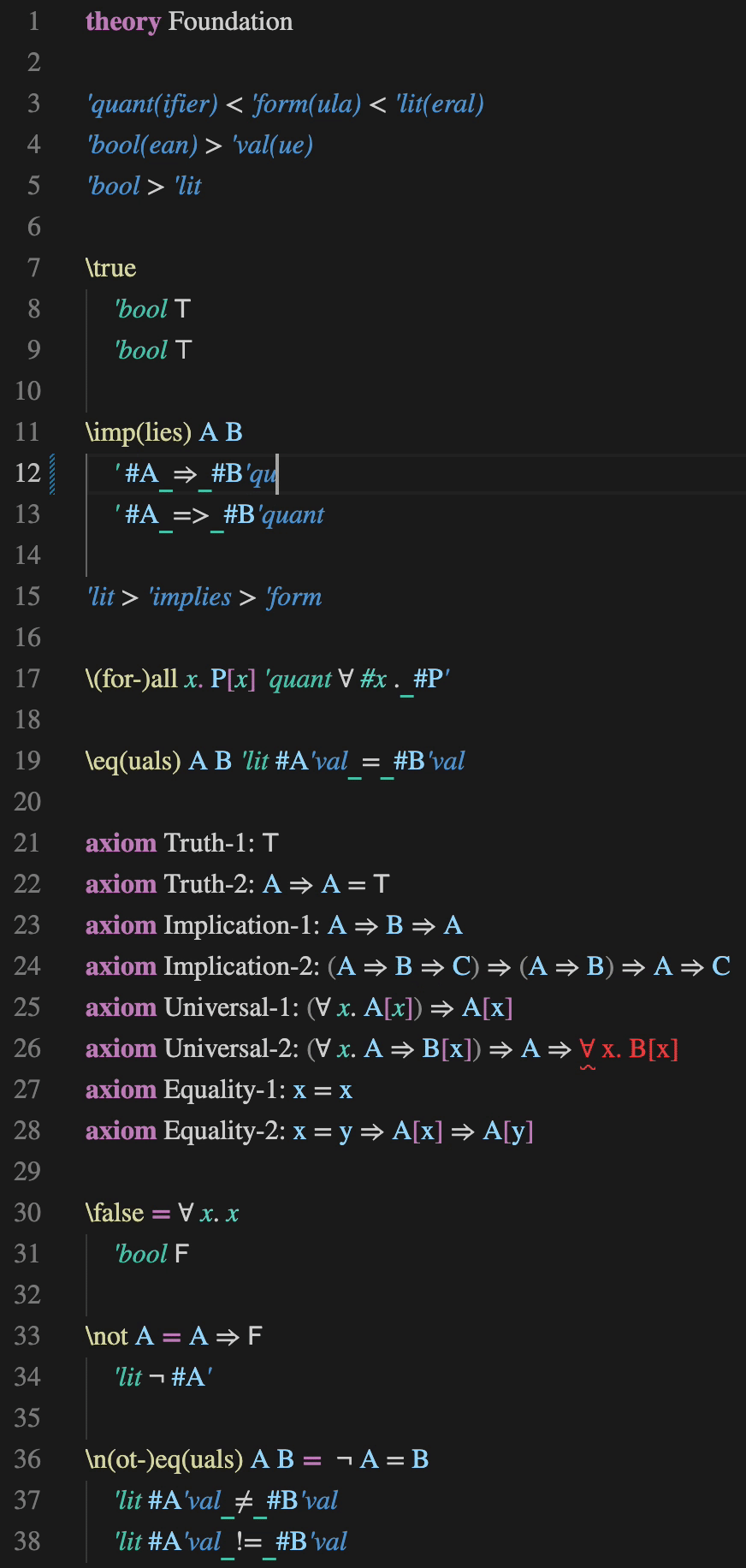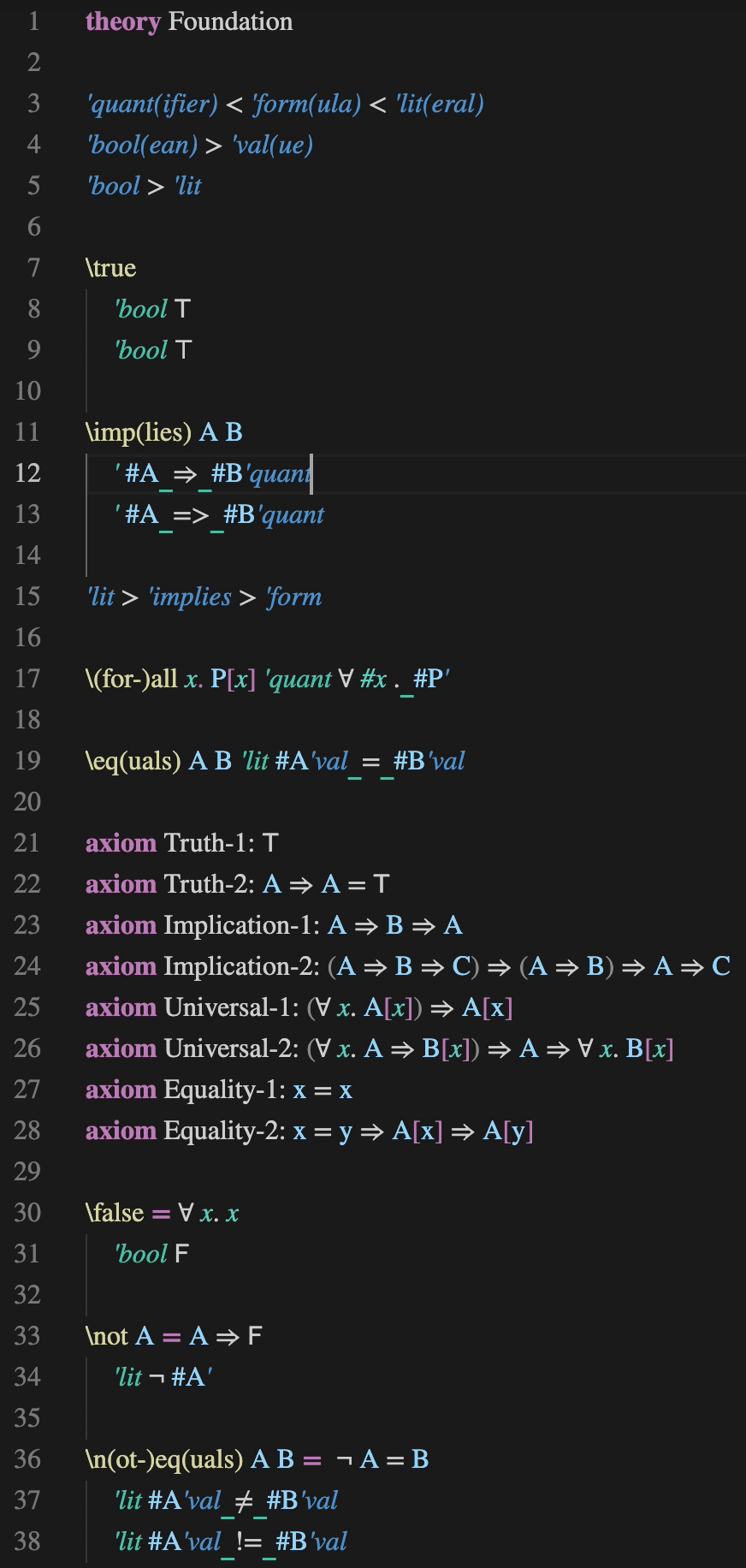
As an example, consider the theory Foundation.practal. This theory will become the root theory of every theory, module and program in Practal. It is displayed on the left, and it might seem that there is a lot going on there in terms of syntax. Practal contains under the hood a full parser generator for deterministic LR parsing based on Local Lexing, which makes it possible to define custom syntax freely. This can be confusing at first, so in this post I will explain the syntax of this file by starting from a version devoid of any custom syntax, but meaning the same, and then progressing in steps to the version with the full custom syntax you see on the left.

Syntax highlighting of Practal code is currently only available from within Visual Studio Code. For this post, I will therefore often display screenshots, but links to the text sources are provided. I encourage you to play with them in VSCode yourself!

Practal comes preconfigured to use STIXGeneral as its text font, but for this to work this font needs to be installed on your system. You can obtain these free STIX fonts from the stixfonts project.

Version 0: No Custom Syntax

The theory file for the version of Foundation.practal without any custom syntax is available here. In VSCode, it displays like this:

First, the theory declares four abstractions: \true, \implies, \for-all, and \equals. As you can see, brackets can be used to indicate abbreviations. Abstraction names are case-insensitive. Hyphens are optional, but may occur at the declared positions only.

An abstraction is really just a name for one of three things:

Obviously, these four abstractions are meant to represent truth, implication, universal quantification, and equality. To capture these meanings, eight axioms are introduced, two for each abstraction. The axioms labelled Truth-1 and Equality-1 are probably the most self-evident of the bunch. The other axioms are also not hard to justify.

You can see that the syntax is reminiscent of LISP and other functional languages. It is really just a prefix notation for expressions. The backslash at the front of abstractions is a nod to (La)TeX, e.g. the expression

\forall x. x

is a valid expression both in Practal and in LaTeX! But while extensive support for displaying Practal terms as LaTeX is planned, the similarities go only so far. For example, the LaTeX expression A \implies B is written \implies A B in Practal instead. Furthermore, typing backslashes can be cumbersome, especially on some international keyboards, and thus the backslash is optional. Finally, it is not necessary to bracket the last parameter of an abstraction:

implies A (implies B C)

can instead be written as

implies A implies B C

Given these declarations and axioms, we can define further abstractions: \false, \not, and \not-equals. It might surprise that \false can be defined via

\false = \for-all x. x

This definition can be explained as follows. Assume \for-all x. x is true. This means that every value x in the mathematical universe is true. This in turn means that every value x in the mathematical universe equals \true. But this means that the mathematical universe consists of a single value only, \true. This is clearly not a very interesting universe, and we call such a single-element universe degenerate. As it turns out, if a theory is true only for degenerate models, then this means that you can prove \for-all x. x in it. Therefore, a theory has only degenerate models if and only if \for-all x. x is a theorem. Thus \false is an apt name for \for-all x. x .

Version 1: Introducing Custom Syntax

Practal’s syntax as described so far is sufficient to express anything you want, and if you can do without custom syntax, you probably should. But if the domain which your abstractions describe has already an established notation, it will be advantageous to define custom syntax in Practal that resembles the established notation. Also, if you are building a library which you expect to get used a lot, it might make sense to define custom syntax for (some of) the abstractions in this library. Clearly, both of these reasons apply for Practal’s foundational theory, and we will thus define custom syntax for its abstractions. This can be done as follows:

To add custom syntax to an abstraction, annotate it with a syntax specification. Such a specification starts with an ASCII apostrophe, and after it comes your custom syntax. For \true in the above example, this is just ' 𝖳. Practal files are text files written in Unicode, so you can use any Unicode character you’d like for your syntax. Here we have chosen the character 𝖳, which has U+1D5B3 as its code and represents a “mathematical sans-serif capital T”. You don’t have to constantly worry about how to type this character, as Practal will soon be able to automatically convert \true to 𝖳 based on your syntax specification (for now, I am using the useful little utility PopChar). Similarly, we represent \false by 𝖥, which is a “mathematical sans-serif capital F” and has code U+1D5A5.

To be able to specify syntax not only for values, but also for operations and operators, you need to be able to refer to the parameters and binders of an abstraction. This is done by prefixing the name of the parameter or binder with a hash character. For \implies, this leads to the syntax specification

' #A  ⇒  #B'

There are several noteworthy things to point out here:

Defining the syntax for \for-all works the same way:

' ∀ #x .  #P

The choice of the symbol ∀ (U+2200) is obvious. This time we refer in our specification not only to the parameter P, but also to the binder x.

Note that with this specification, nested universal quantifiers need brackets, as in

∀ x. (∀ y. Q[x, y])

To avoid this, we could have just used #P' instead of #P in our specification. But this would not have helped with a formula like

∀ x. (∃ y. Q[x, y])

assuming that later on we might want to introduce another quantifier ∃. Actually, it already does not help with the formula

∀ x. (x = x)

where we would like to drop the brackets around the equality, but cannot. Similarly,

(x = y) ⇒ A[x] ⇒ A[y]

should also not require any brackets around the equation.

In order to deal with these issues, Practal provides the concept of syntactic categories.

Syntactic Categories

In systems like Isabelle custom syntax can be defined by assigning priorities to expressions, and to holes in expressions. A priority in Isabelle is just a number, and therefore two priorities are always comparable. A similar approach is taken by Vaughan Pratt in his 1973 paper “Top Down Operator Precedence”:

The idea is to assign data types to classes and then to totally order the classes. An example might be, in ascending order, Outcomes (e.g., the pseudo-result of “print”), Booleans, Graphs (e.g. trees, lists, plexes), Strings, Algebraics (e.g. integers, complex nos, polynomials, real arrays) and References (as on the left side of an assignment.) We write Strings < References, etc.

A difference between Isabelle and Pratt’s approach is that Pratt uses names for priority classes instead of just raw numbers. They are similar though in that both approaches insist on a total order on priorities.

Inspired by Pratt’s approach, Practal also uses names for priority classes. Such a name is called a syntactic category. But we do not insist that syntactic categories are totally ordered. Instead, we incorporate an idea advocated by Danielsson and Norell in their 2011 paper “Parsing Mixfix Operators”: Priorities should form a directed acyclic graph (DAG). Their argument is a convincing one:

Many languages require the precedence relation to be a total order. However, this can make reading source code more difficult, because it means that every operator is related to every other, which is likely to make it harder for programmers to remember the precedence relation. It also means that one needs to make unnecessary, possibly arbitrary choices. Why should one have to specify a relation between + and ∧ , two semantically unrelated operators, for instance? This goes against modularity. One might think that partial orders are a good alternative. However, under the (reasonable) assumption that + binds tighter than == , which binds tighter than ∧ , transitivity would imply that + binds tighter than ∧ , which we want to avoid.

Nevertheless, partial orders are often useful for specifying priority relations. This is not a problem, as a partial order is just a particular kind of DAG. In Practal, we employ therefore two kinds of relations between syntactic categories A and B, which are then merged to result in a DAG ≺:

The relation A ≺ B is defined as follows: A ≺ B if and only if you can get from A to B via < and ⪪, where you can hop via < as many times as you like, but via ⪪ at most one time. We enforce that A ≺ B is always acyclic and therefore forms a DAG.

Applying Practal to the scenario described by Danielsson and Norell yields:

Three binary abstractions \plus, \eq and \and are introduced, where \plus is left-associative and \and is right-associative. These abstractions have implicit syntactic categories 'plus, 'eq and 'and. Actually, writing

\plus x y ' #x' + #y

is just short for

\plus x y 'plus #x' + #y

which in turn is short for

\plus x y 'plus #x'plus + #y'greater-than-plus

The category 'greater-than-plus exists internally, but is not user-accessible. It is the collection of all syntactic categories S such that 'plus ≺ S.

This way, each custom syntax expression has a syntactic category associated with it, and each hole/parameter in a custom syntax expression has a syntactic category associated with it as well. Just like with Pratt’s approach, you can then plug an expression of category B into a hole labelled with category A only iff A = B or A ≺ B holds.

The declaration

'plus ⪫ 'eq ⪫ 'and

then means that 'and ≺ 'eq and 'eq ≺ 'plus both hold, but that 'and ≺ 'plus does not hold. Accordingly, we can write x == x ∧ x + y == y + x, but we are not allowed to write x + y ∧ y + x . If we were to replace one (or both) of the ⪫ by >, then 'and ≺ 'plus would hold as well, and the expression x + y ∧ y + x would now be allowed.

Final Version

Armed with syntactic categories, we are now ready for the (currently) final version of Foundation.practal:

We introduce five explicit syntactic categories:

We want ∀ x. A = B ∧ C to mean ∀ x. ((A = B) ∧ C), and therefore introduce the following priorities:

'quantifier < 'formula < 'literal

Booleans play a double role. On one hand, they certainly are values, and so it makes sense to declare

'boolean > 'value

On the other hand, they can also be interpreted as atomic formulae, and thus:

'boolean > 'literal

We put 𝖳 and 𝖥 into the 'boolean category, and let =, ¬ and ≠ construct 'literal expressions. That leaves implication, which we place between literals and formulae via

'literal > 'implies > 'formula

This leaves room for later being able to add properly prioritized custom syntax for other logical operators such as \and and \or.

It is possible to define multiple custom syntax variants for a single abstraction, and we take advantage of this to provide easier to type syntax variants for implication and inequality. We also introduce an additional symbol ⊤ (U+22A4) for \true, as it is commonly used for this purpose. We don’t use ⊥ for \false though, as we intend to use this symbol to denote undefinedness, or rather failure. But this will be the topic of another post.

Post Scriptum

While writing the previous section, I started wondering why the final version of Foundation.practal does not make any use of ⪪ . I believe now that in the context of Practal, partial orders are enough and the generality of DAGs is not needed. The reason is that Practal does not do pure operator precedence parsing, but instead constructs fairly general context-free grammars, although guided by priorities. The argument put forward by Daniellson and Norell, which I previously found so convincing, is actually easily countered: the syntactic category of an expression does not need to be related priority-wise to the syntactic categories of its holes. In particular, consider the custom syntax for equality:

'literal #A'value = #B'value
The category of such an equality expression is 'literal, which is not related to the category of any of its two holes, which is 'value in both cases. We can therefore reformulate the example of Daniellson and Norell as follows in Practal:

Using just partial orders instead of DAGs is simpler, and future versions of Practal will therefore most likely drop the support for ⪪ .

If you’ve read so far, and like the direction Practal is going, please consider sponsoring Practal. I am now working full-time on Practal, and would like to continue to do so! I am also happy to give talks about Practal and Abstraction Logic either remotely or on-site. If you’d like to leverage Practal for your business, I am available for consulting services. I speak both English and German, and am happy to communicate in either of these languages.

You can contact me either through Practal’s sponsoring page, or directly via hi@practal.com.